Various properties of superconductors are described in the article 'The Language of Superconductor Physics' , and also explored in the preceding sections of the laboratory experiments. One of the most basic applications of the fundamental properties of a superconductor is exploiting its complete absence of resistance to an electrical current flow. This property has been exploited in superconducting energy storage rings being designed by the U.S. Navy called SMES (Superconducting Magnetic Energy Storage) project, and also in studies by electric power utilities for base load power storage for commercial electric power generation.
The Superconducting Energy Storage Kit from Colorado Superconductor Inc. demonstrates the fundamentals of energy storage in superconducting rings. The basis of this Kit is a toroidal ring made from a high temperature superconductor. A current can be induced in the toroid, and because of its superconducting nature, the current can potentially persist for an extremely long time. A powerful cylindrical magnet is provided with the kit for induction of a persistent current. A large magnetic compass is provided as a detector of persistent currents. The compass is in four parts, but can be reassembled following the directions provided with it.
The experiment described in the following paragraphs can be performed with no additional equipment except for liquid nitrogen and a suitably deep container for immersing the toroid in. However, should one be available, a Hall-probe Gaussmeter can substantially enhance the quality of the results of this experiment.
Persistent Current Demonstration
- ACTION
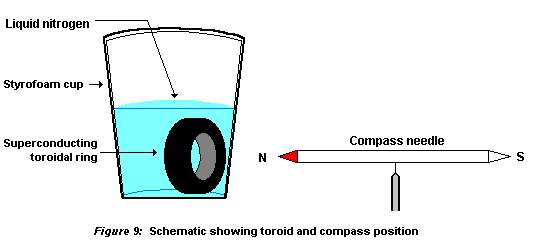
Place the toroidal ring in a 1.5 inch high section of the bottom of a styrofoam coffee cup, or the rectangular cavity in the Kit container. The cavity should be deep enough that the toroid can be completely immersed even when it is standing on its edge. - ACTION
With the toroid flat at the bottom of the styrofoam container, place the pole of the cylindrical magnet in close proximity, above or below the hole of the toroidal ring. - ACTION
Immerse the superconducting toroid in a bath of liquid nitrogen.
RESULT
The liquid nitrogen boils furiously. Wait until the boiling subsides. - ACTION
Carefully move the magnet, crossing any one side of the toroid. The magnet or toroid may be moved relative to each other. Take care not to withdraw the toroid for more than a few seconds out of the liquid nitrogen bath while performing this action. Remove and store the magnet in a far corner of the room. Several other techniques for moving the magnet relative to the toroid have been found to work. We encourage you to experiment. - ACTION
Using the provided non-magnetic tweezers, carefully turn the toroid on edge so that the axis of the toroid is horizontal. Orient the liquid nitrogen container so that the axis of the toroid is in the earth's magnetic east-west direction. Again take care that no part of the toroid emerges above the surface of the liquid nitrogen. - ACTION
After establishing an identification of the faces of the toroid, carefully bring a needle tip of the provided compass close to the axis of the toroid. The liquid nitrogen container with the toroid may need to be elevated to facilitate this action. Also, great care must be exercised that there are no magnetic or ferromagnetic objects near the compass or toroid. The liquid nitrogen container walls will be in between the toroid and the compass, but this should pose no problems since the walls are thin, and are made from a non-magnetic material.
RESULT
The compass needle will be either repelled or attracted by the toroid. - ACTION
Present the other pole of the compass needle to the same face of the toroid.
RESULT
This time the repulsion/attraction action of the previous result will be reversed. If the Meissner Effect or the Suspension Effect were responsible for the repulsion or attraction of the compass needle, this reversal would not have been observed.
Some questions
- What happens when you remove the toroid from the liquid nitrogen bath and repeat an attempt to deflect the compass needle?
- Is one application of this effect a powerful permanent magnet? If so, what are its advantages and limitations over existing permanent magnets?
- If you repeat this experiment but do not use a magnet to induce an electrical current in the toroid, what are the compass needle deflection results that you would expect to see?
- Could you use this phenomena to estimate the Critical Temperature? If so, how?
- Can you design a system for withdrawing the electrical energy out of our storage ring toroid for use?
- What are some other potential applications of the persistent electrical current in a toroidal coil?
The amount of deflection of the compass needle can be used to obtain a rough measurement of the current that has been induced in the toroid. The provided scale with compass will allow one to obtain the value of the deflection. The deflection will have to be corrected for the Meissner Effect by successively measuring the deflection for either the two different poles of the compass needle, or the deflection caused by the two faces of the toroid for the same pole of the compass needle. Please see figure 9 below for the positioning of the experimental components. Figure 10 shows the different variables and the configuration of the compass needle and toroid.
Estimation of the value of the induced current
The induced superconducting current represents a stored electric current, and can be shown to persist for extremely long periods of time as long as the toroidal ring is kept at liquid nitrogen temperatures. If this experiment were to be scaled up in size, the stored electrical energy could potentially be used at any later time. This is the principle of the U.S. Navy's SMES experiment.
This semi-quantitative measurement of the persistent current in the toroid requires an estimation of the deflection of the needle (shown as the angle ø in figure 10 above), and the distance of the needle tip from the center of the toroid (distance x in figure 10). The deflection of the compass needle at distance 'x' from the toroid, is the result of a combination of forces exerted by the horizontal component of earth's magnetic field (ßearth) and the magnetic field due to the toroid (ßtoroid). The relation between these quantities is simply
ßtoroid = ßearth tanø
The horizontal component of the earth's magnetic field is about 2 X 10-4 Tesla (2 Gauss). This value varies slightly with one's position on the earth. From this estimation of the magnetic field of the toroid, the Biot-Savart Law or Ampere's can be used to calculate the current induced (Itoroid) and extant in the toroid.
Itoroid = (2ßtoroid(x2 + r2)3/2)/µr2
Here 'r' is the average radius of the toroid and is approximately 0.0095 meters (see figure 10), and µ is the permeability of free space and is equal to (4*pi) X 10-7 Newton/Amp2.
r = raverage = (Outer diameter + Inner diameter)/4
All units in this form of the Biot-Savart Law are SI (Standard International) units. Distances x and r are in meters, magnetic field strength ß is in Tesla, and Current I is in Amperes.
The amount of current in the toroid (Itoroid), can be increased by increasing the strength of the magnet used to induce the current. However, the magnet that has been provided is already one of the most powerful commercially available magnets. Several passes in the same direction with a magnet should also work. Use of an electromagnet for inducing the current in the toroid may offer the best solution.
Instead of using a compass to determine the magnetic field of the toroid, a Hall-probe Gaussmeter can be used for a much more accurate measurement. This approach has the added advantage that the toroidal ring superconductor can remain in a horizontal position throughout the experiment.
Estimation of the lifetime of the persistent current.
The existence of a persistent current in the toroidal ring has already been amply demonstrated by our compass needle deflection experiment. However, it would be instructive to actually attempt to measure the decay of the electrical current as a function of time.
The initial expectation is that there should simply be no decay of the persistent electrical current over time since, after all, the toroid is a superconductor, and exhibits no electrical resistance, and hence no energy loss. Practically however, on account of the phenomena of flux creep and flux flow one will see a very small exponential decay of the stored electrical current. It would be very instructive to investigate this decay because it provide an insight into the effective `resistance' of the superconducting toroid.
The simplest approach is to first induce an electrical current in the toroid as per the procedure described above. It is however recommended that you should use a Gaussmeter for this experiment on account of the precise measurements that are required. The toroid with its induced persistent current will then have to be stored at liquid nitrogen temperatures over a period of several weeks. The current in the toroid is measured at periodic intervals over this time. Care will need to be exercised to prevent heating any portion of the toroid during the duration of the investigation.
If the results of measurement of the electrical current in the toroid were plotted versus the time intervals over which these measurements were made, it will be seen that the current decays exponentially as a function of time as described the following relationship
e-(R/L)t = F
Where R is the electrical resistance of the toroid, L is the inductance of the toroid, and F is the fraction of the remaining electrical current at time t. Our own measurements indicate that for the toroidal ring in the Superconducting Energy Storage Kit, the value of L is about 5 nH (nano Henry). Using this number we have obtained a value of the toroid ring electrical resistance equal to 10-15 ohms.
Working backwards, using the measured value of R above, the time required for the current to decrease to 50% of its original value, we find that
tI=0.5 = 1023 years
Note: This is an approximate value.
This indicates that for most practical purposes, the current is permanently stored in the toroidal ring superconductor.
The experiments and descriptions above have been drawn from experimental procedures described by Dr. Donald L. Shirer of the Physics Department at Yale University and Dr. Peter Heller and his colleagues at Brandeis University. An excellent treatment of these experiments can be found in the article entitled `Nitrogen Temperature Storage Ring Experiment' by F. Liu, R.R. Tucker, and P. Heller appearing in the American Journal of Physics, March 1990.
Information Courtesy of CSI Superconductors

